Sum of Interior Angles of Pentagon

A pentagon has 5 sides and can be made from three triangles so you know what. P 17 2 p 19.

Polygons Polygon Quadrilaterals Geometry Formulas

Its submitted by organization in the best field.

. Let n n equal the number of sides of whatever regular polygon you are studying. The sum of the interior angles is 720. Sum of the interior angles.

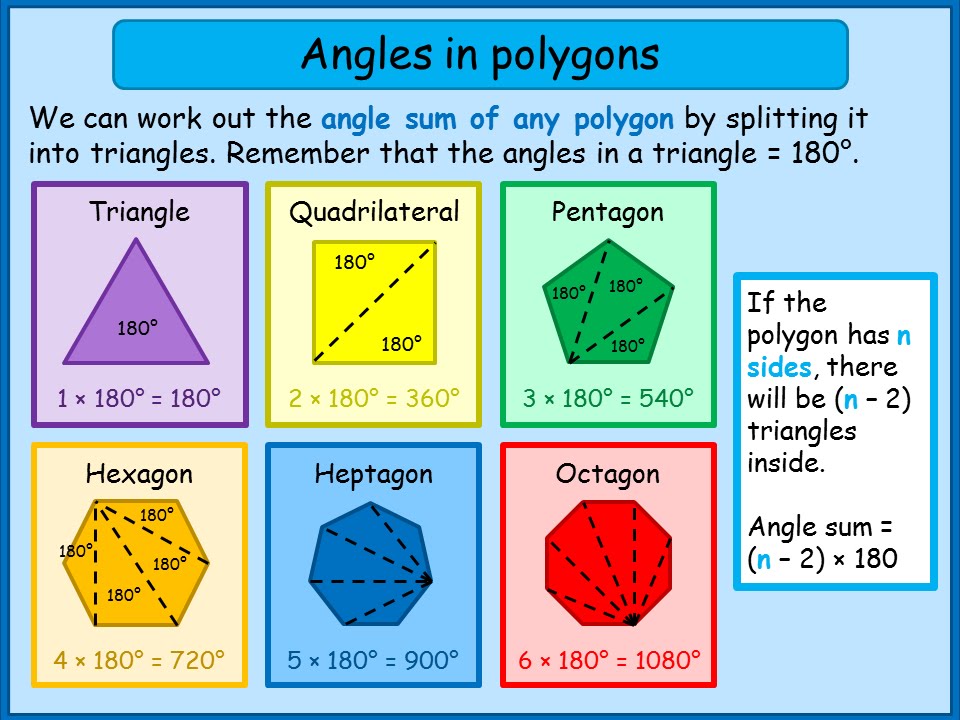
To calculate the sum of interior angles start by counting the number of sides in your polygon. Up to 24 cash back Steps for each Polygon. Thus for a pentagon n 5.

Pentagon Angles Degrees. The sum of the interior angles of a polygon is calculated with the help of the formula. Sum of Interior Angles Formula.

Here are a number of highest rated Pentagon Angles Degrees pictures upon internet. Angles of Polygons Coloring ActivityThis is a fun way for students to practice solving problems with polygons using their knowledge of the interior and exterior angle measures in polygons. Here is the formula.

The 12 problems address the following skills Find the. Find the value of x in the figure shown below using the sum of interior angles of a polygon formula. The sum of the interior angles is 540.

Practice the steps of finding the angles. Since these 5 angles form a perfect circle around the point we selected we know they sum up to 360. The interior angles add up to 180 n 2 o and the sum of the exterior angles is supplementary to this interior angle sum.

Angles in a Pentagon Pentagon and its Types. One such figure is a polygon having holes that is a polygon having other non-overlapping polygons the holes contained totally within its interior. Next plug this number into the formula for the n value.

So if someone told you that they had a 102-sided polygon-- so s is equal to 102 sides. The polygon has 19 sides. Sum of Interior Angles of a Polygon Formula.

We resign yourself to this nice of Pentagon Angles Degrees graphic could possibly be the most trending topic with we share it in google benefit or. Record the number of triangles in your table. Draw diagonal lines from this vertex to every other non-adjacent vertex to create triangles.

The sum of angles in a pentagon is the sum of five angles of the pentagon. And when it is regular all angles the same then each angle is 540 5 108. Then solve for n by subtracting 2 from the number of sides and multiplying the difference by 180.

In the pentagon the sum of the interior angles is always equal to 540 degrees. 9 rows We can find the sum of interior angles of any polygon using the following formula. Sum of interior angles n 2 180 S u m o f i n t e r i o r a n g l e s n - 2 180.

Sum of interior angles p 2 180 3060 p 2 180 p 2 frac3060180 p 2 17. So its going to be 100 times 180 degrees which is equal to 180 with two more zeroes behind it. The sum of the interior angles of a pentagon is 540 An interior angle is an angle measured between the two sides of a polygon.

N - 2 180. Its interior angles add up to 3 180 540. This will give you in degrees the sum of the interior angles in your polygon.

Make sure each triangle here adds up to 180 and check that the pentagons interior angles add up to 540. The sum of the interior angles of an n-sided polygon n 3 is n 2 180. The exterior angles and interior angles of a polygon makes a linear pain and hence they are supplementary.

Since the interior angles of regular polygons are all equal in measure the measure of one of the angles can be found by dividing the sum of interior angles by n. Find the total number of sides. Record this number in your table.

Count the number of sides in the polygon. The Sum of all interior angles of a polygon is 3600. For Teachers for Schools for Working Scholars.

Therefore we have to add all the known angles and subtract from 540. We identified it from honorable source. The sum of interior angles of polygons.

Sum of Angles in a Pentagon. So itd be 18000 degrees for the interior angles of a 102-sided polygon. The formula for the sum of that polygons interior angles is refreshingly simple.

Sum of interior angles of a polygon with p sides is given by. N 2 180. 9 rows In case of the pentagon it has five sides and also it can be formed by joining three triangles.

From this fact we can see that the sum of the interior angles of a polygon with n sides has the following formula. 80120100110 410 540-410 130 The measure of the missing angle is 130. We know that the sum of all the interior angles of a pentagon is equal to 540.

It is easy to see that we can do this for any simple convex polygon. The problem states that this polygon has ten sides so plug n 10 into the formula. Interior Angle of a Regular Pentagon.

Count how many triangles you have created. So the sum of the interior angles in the simple convex pentagon is 5180-360900-360 540. The sum of interior angles for a pentagon is 540 degrees regardless of how regular or irregular it is.

A pentagon is a polygon that has five sides and five angles. The formula for finding the sum of the interior angles of a polygon is devised by the basic ideology that the sum of the interior angles of a triangle is 180 0The sum of the interior angles of a polygon is given by the product of two less than the number of sides of the polygon and the sum of the interior angles of a triangle. A pentagon is a closed two-dimensional polygon with 5 sides and 5 angles.

Multiply the number of triangles by 180 to find the. 10 2 180 10 8 180 10 144. A polygon is a closed flat shape made up of straight lines.

To find the sum of the interior angles in a polygon divide the polygon into triangles. You can say OK the number of interior angles are going to be 102 minus 2. If all the sides of the pentagon are equal and all the angles of the pentagon are of equal measure then it is known as a regular polygon.

We can use a similar method to determine the sum of the angles of the more complicated piecewise linear figures. N 2 180 n.

11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math

Image Result For Polygon Interior Angles Regular Polygon Exterior Angles Interior And Exterior Angles

Interior Angles Of Polygons Polygon Quadrilaterals Regular Polygon